The Hartmann mask is a simple and cheap tool to focus a telescope for photography. Take a cardboard disk with the diameter of the telescope's optic, cut two (or three) holes in it and place it in front of the telescope. If the telescope is out of focus then two stars in a certain distance of each other are seen for any single star. When approaching focus the distance of the two star images decreases until they meet in the focus and only single stars can be seen. This design was improved to a modified Hartmann mask with a vertical and a horizontal slit instead of the two round holes. Although this cross slit mask is a big improvement there might some cases where it might be not precise enough. This is why I tried to find experimentally a slit geometry that makes it easier to decide when both slits meet exactly in their centers. The geometry was systematically modified with the target that at focus a vertical slit crosses a X-shaped slit exactly in its center.

On the left side you can see the shape of the mask followed by three images of a bright star during focusing. First the star is well out of focus, next it is close to the focus and finally in focus. While out of focus the star image resembles the shape of the mask this changes when approaching the focus. Already close to the focus spikes are visible which become strong and sharp at focus. The spikes show even a brightness variation. The spikes are diffraction patterns caused by the diffraction of the light at the slit edges. Out of focus the spikes are double and at focus narrow and with varying brightness. I was quite surprised that the vertical slit produced a horizontal spike.

To analyse this unexpected phenomenon I changed the mask a little bit. The result can be seen above. At the focus the orientation of the spikes is perpendicular to the slits. This explains why I never noticed this effect with the horizontal and vertical arrangement of the slits because in this case the spikes replaced the images of the slits.

Now it is clear the single slit has to be cut horizontally to produce a vertical spike at the focus. The simplest way to achieve that was to cut a cross like a pluss sign in my mask. Et voilá: A vertical spike crosses the other spikes in their center. But how much would the vertical spike move when the focuser is moved slightly in and out of focus? Would that be noticeable?

The sequence above shows the result of the experiment where the focuser was slightly moved inward and outward. The vertical spike changes its position significantly in relation to the cross center of the other spikes. Mission accomplished! It can be noticed that the spikes are sharper and their brigthness variation is more pronounced the better the focus is met.

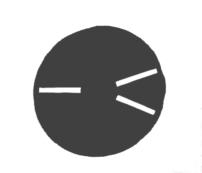
The experiments showed that the vertical slit is obsolete and only the horizontal slit is essential. Consequently I changed my masks for the refractor (left) and the C9.25 (right) as seen above. For the C9.25 I cut the slits that should form an X separately into the mask because the cross angle of the slits would have compromised the mechanical stability of the mask. Now the shape of the slits resembles a horizontally lying Y.

IT'S PURE PHYSICS:

I already mentioned it: The phenomenon we see here is called diffraction at a slit edge. A point light source, as which we can regard every star (a laser beam would also do the job), is split into a chain of images at a right angle to the edge. The intensity (i.e. the brightness) of the images drops with increasing distance from the edge. The distance of the images is dependent of the slit width.

The same physics apply if the light of a star falls through a concentric aperture. The result are concentric images of the point light source which become fainter the farther they are from the center. This phenomenon we know as diffraction rings of stars seen in our telescopes at high magnification!

By the way: The parallel arrangement of multiple slits, i.e. a grate, does not change the effect but increases the intensity of the images of the spikes. Such a modification of the slit mask is known as Bahtinov mask. As you may guess it is easier to make yourself a slit mask (as desribed above) than to make a Bahtinov mask because in the latter case it is essential that the edges of all three groups of slits are parallel. Edges that deviate from the correct angle will blur the spikes.